Curs 2015-16



CFA Cornellà
El racó de la Silvia
Els nombres reals inclouen aquells que es poden expressar de forma de fracció (nombres racionals) i aquells que tenen infinites xifres decimals no periòdiques i no es poden representar en forma de fracció (nombres irracionals).
Els nombres naturals són els primers nombres que es van utilitzar, ja que serveixen per comptar i ordenar. El conjunt dels nombres naturals està format per:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ...}
1.Els nombres naturals estan ordenats: el que ens permet comparar dos nombres naturals: 5>3 ; 5 és major que 3. 3 <5 ; 3 és menor que 5.
2.Els nombres naturals són il·limitats: si a un nombre natural li sumem 1, obtenim un altre nombre natural.
3.Representació dels nombres naturals: Els nombres naturals es poden representar en una recta ordenats de menor a major. Sobre una recta assenyalem un punt, que marquem amb el número zero. A la dreta del zero, i amb les mateixes separacions, situem de menor a major els següents nombres naturals: 1, 2, 3 ..
4.Operacions bàsiques amb nombres naturals: Les operacions bàsiques que podem fer amb nombres naturals són: La suma, la resta, la multiplicació, la divisió, la potencia i l'arrel
-
Suma de nombres naturals: a + b = c (Els termes de la suma, a i b, es diuen sumands i el resultat, c, suma.)
-
Resta de nombres naturals: a-b =c (a és el minuend, b és el subtrahend, c és la resta o diferència) La suma i la resta són operacions inverses.
-
Multiplicació de nombres naturals: a·b = c (a és el factor 1, b és el factor 2, c és el producte)
-
Divisió de nombres naturals a:b = c (a és el dividend, b és el divisor, c és el quocient)
La multiplicació i la divisió són operacions inverses
5. Propietats de les operacions
-
Interna: El resultat d'operar amb dos nombres naturals és sempre un altre nombre natural. Aquesta propietat la compleixen la suma i la multiplicació però no la resta i la divisió
-
Associativa: La manera d'agrupar els valors amb els que s’està operant no varia el resultat. Aquesta propietat la compleixen la suma i la multiplicació però no la resta i la divisió
(a + b) + c = a + (b + c) Ex: (2 + 3) + 5 = 2 + (3 + 5) = 10
(a · b) · c = a · (b · c ) Ex: (2 · 3) · 5 = 2 · (3 · 5) = 30
-
Commutativa: L'ordre en que operem els valors no canvia el resultat.
a + b = b + a Ex: 2 + 5 = 5 + 2
a · b = b · a Ex 6 · 5 = 5 · 6 = 30
Aquesta propietat la compleixen la suma i la multiplicació però no la resta i la divisió
-
Element neutre: El 0 és l'element neutre de la suma i de la resta perquè tot nombre sumat o restat amb ell dóna el mateix nombre.
a + 0 = a Ex: 3 + 0 = 3
a - 0 = a Ex 7 - 0 = 7
L'1 és l'element neutre de la multiplicació i de la divisió, perquè tot nombre multiplicat o dividit per 1 dóna el mateix nombre. a · 1= a Ex: 7 . 1 = 7 ; a : 1 = a Ex: 75 : 1 = 75
-
Propietat distributiva: Aquesta propietat relaciona la multiplicació amb la suma i la resta:
a · (b + c ) = a · b + a· c
-
Potències de nombres naturals: Una potència és una forma abreujada d'escriure un producte format per diversos factors iguals.
-
La base d'una potència és el nombre que multipliquem per si mateix, en aquest cas el 5.
-
L'exponent d'una potència és el nombre de vegades que multipliquem la base, en l'exemple és el 4.
-
Però no es possible fer restes amb ells, on el minuend es mes petit que el subtrahend. Com a la vida real ens trobem amb operacions d'aquest tipus: on a un nombre menor cal restar li un de més gran. Per exemple: si tens 10 euros i en deus 15, de quants diners disposes? Igual passa per representar temperatures sota zero, profunditats respecte al nivell del mar, etc.
Ens vam veure obligats a ampliar el concepte de nombres naturals, introduint un nou conjunt numèric anomenat nombres enters. El conjunt dels nombres enters es representa amb la lletra Z i està format per:
Z={...-5, 4,- 3,- 2, -1, 0, 1, 2, 3, 4, 5...}
Els nombres enters es divideixen en tres parts: enters positius o nombres naturals, enters negatius i zero.
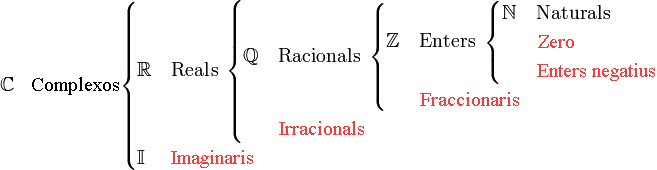
ELS NOMBRES



ORDRE D'OPERACIONS COMBINADES
-
Efectuar les operacions entre parèntesis, claudàtors i claus.
-
Calcular les potències i arrels.
-
Efectuar els productes i quocients (D’ESQUERRA A DRETA).
-
Realitzar les sumes i les restes (D’ESQUERRA A DRETA).
